| Type: | Package |
| Title: | Provides Tools for Working with General Simplicial Complexes |
| Version: | 1.0.1 |
| Date: | 2020-08-25 |
| Depends: | R (≥ 3.4.0) |
| Maintainer: | Matt Piekenbrock <matt.piekenbrock@gmail.com> |
| Description: | Provides an interface to a Simplex Tree data structure, which is a data structure aimed at enabling efficient manipulation of simplicial complexes of any dimension. The Simplex Tree data structure was originally introduced by Jean-Daniel Boissonnat and Clément Maria (2014) <doi:10.1007/s00453-014-9887-3>. |
| Language: | en-US |
| License: | MIT + file LICENSE |
| URL: | https://github.com/peekxc/simplextree |
| LinkingTo: | Rcpp |
| Imports: | Rcpp (≥ 0.12.10), methods, magrittr |
| Encoding: | UTF-8 |
| LazyData: | true |
| SystemRequirements: | C++11 |
| RoxygenNote: | 7.1.0 |
| Suggests: | testthat, knitr, rmarkdown, covr |
| NeedsCompilation: | yes |
| Packaged: | 2020-09-09 22:00:17 UTC; mpiekenbrock |
| Author: | Matt Piekenbrock [cre, aut], Jason Cory Brunson [ctb], Howard Hinnant [cph] |
| Repository: | CRAN |
| Date/Publication: | 2020-09-12 12:20:02 UTC |
simplextree package
Description
Provides an R/Rcpp implementation of a Simplex Tree data structure and its related tools.
Details
This package provides a lightweight implementation of a Simplex Tree data structure, exported as an Rcpp Module. The current implementation provides a limited API and a subset of the functionality described in the paper.
Author(s)
Matt Piekenbrock
Pipe operator
Description
See magrittr::%>% for details.
Usage
lhs %>% rhs
Adjacent vertices.
Description
Returns a vector of vertex ids that are immediately adjacent to a given vertex.
Usage
adjacent(st, vertices)
Arguments
st |
a simplex tree. |
vertices |
vertex ids. |
Examples
st <- simplex_tree(1:3)
st %>% adjacent(2)
# 1 3
as.list.st_traversal
Description
as.list.st_traversal
Usage
## S3 method for class 'st_traversal'
as.list(x, ...)
Arguments
x |
traversal object. |
... |
unused. |
Clears the simplex tree
Description
Removes all simplices from the simplex tree, except the root node.
Usage
clear(st)
Arguments
st |
a simplex tree object. |
Examples
st <- simplex_tree()
st %>% insert(1:3)
print(st) ## Simplex Tree with (3, 3, 1) (0, 1, 2)-simplices
st %>% clear()
print(st) ## < empty simplex tree >
Clones the given simplex tree.
Description
Performs a deep-copy on the supplied simplicial complex.
Usage
clone(st)
Arguments
st |
a simplex tree. |
Generates a coface roots traversal on the simplex tree.
Description
The coface roots of a given simplex sigma are the roots of subtrees
in the trie whose descendents (including the roots themselves) are cofaces of sigma.
This traversal is more useful when used in conjunction with other traversals, e.g. a preorder
or level_order traversal at the roots enumerates the cofaces of sigma.
Usage
coface_roots(st, sigma)
Arguments
st |
the simplex tree to traverse. |
sigma |
simplex to start the traversal at. |
Generates a coface traversal on the simplex tree.
Description
Generates a coface traversal on the simplex tree.
Usage
cofaces(st, sigma)
Arguments
st |
the simplex tree to traverse. |
sigma |
simplex to start the traversal at. |
Elementary collapse
Description
Performs an elementary collapse.
Usage
collapse(st, pair, w = NULL)
Arguments
st |
a simplex tree. |
pair |
list of simplices to collapse. |
w |
vertex to collapse to, if performing a vertex collapse. |
Details
This function provides two types of elementary collapses.
The first type of collapse is in the sense described by (1), which is
summarized here. A simplex \sigma is said to be collapsible through one of its faces \tau if
\sigma is the only coface of \tau (excluding \tau itself). This function checks whether its possible to collapse \sigma through \tau,
(if \tau has \sigma as its only coface), and if so, both simplices are removed.
tau and sigma are sorted before comparison.
To perform this kind of elementary collapse, call collapse with two simplices as arguments, i.e. tau before sigma.
Alternatively, this method supports another type of elementary collapse, also called a vertex collapse, as described in (2). This type of collapse maps a pair of vertices into a single vertex. To use this collapse, specify three vertex ids, the first two representing the free pair, and the last representing the target vertex to collapse to.
Value
boolean indicating whether the collapse was performed.
References
1. Boissonnat, Jean-Daniel, and Clement Maria. "The simplex tree: An efficient data structure for general simplicial complexes." Algorithmica 70.3 (2014): 406-427.
2. Dey, Tamal K., Fengtao Fan, and Yusu Wang. "Computing topological persistence for simplicial maps." Proceedings of the thirtieth annual symposium on Computational geometry. ACM, 2014.
Examples
st <- simplextree::simplex_tree(1:3)
st %>% print_simplices()
# 1, 2, 3, 1 2, 1 3, 2 3, 1 2 3
st %>% collapse(list(1:2, 1:3))
# 1, 2, 3, 1 3, 2 3=
st %>% insert(list(1:3, 2:5))
st %>% print_simplices("column")
# 1 2 3 4 5 1 1 2 2 2 3 3 4 1 2 2 2 3 2
# 2 3 3 4 5 4 5 5 2 3 3 4 4 3
# 3 4 5 5 5 4
# 5
st %>% collapse(list(2:4, 2:5))
st %>% print_simplices("column")
# 1 2 3 4 5 1 1 2 2 2 3 3 4 1 2 2 3
# 2 3 3 4 5 4 5 5 2 3 4 4
# 3 5 5 5
Edge contraction
Description
Performs an edge contraction.
Usage
contract(st, edge)
Arguments
st |
a simplex tree. |
edge |
an edge to contract, as a 2-length vector. |
Details
This function performs an edge contraction in the sense described by (1), which is
summarized here. Given an edge {va, vb}, vb is contracted to va if vb is
removed from the complex and the link of va is augmented with the link of vb. This may be thought as
applying the mapping:
f(u) = va
if u = vb
and identity otherwise, to all simplices in the complex.
edge is not sorted prior to contraction: the second vertex of the edge is always contracted to the first.
Note that edge contraction is not symmetric.
References
1. Boissonnat, Jean-Daniel, and Clement Maria. "The simplex tree: An efficient data structure for general simplicial complexes." Algorithmica 70.3 (2014): 406-427.
Examples
st <- simplex_tree(1:3)
st %>% print_simplices()
# 1, 2, 3, 1 2, 1 3, 2 3, 1 2 3
st %>% contract(c(1, 3)) %>% print_simplices()
# 1, 2, 1 2
The vertex degree.
Description
Returns the number of edges (degree) for each given vertex id.
Usage
degree(st, vertices)
Arguments
st |
a simplex tree. |
vertices |
the vertex ids to check the degree of. |
Deserializes the simplex tree.
Description
Provides a compressed serialization interface for the simplex tree.
Usage
deserialize(complex, st = NULL)
Arguments
complex |
The result of |
st |
optionally, the simplex tree to insert into. Otherwise a new one is created. |
Details
The serialize/deserialize commands can be used to compress/uncompress the complex into
smaller form amenable for e.g. storing on disk (see saveRDS) or saving for later use.
See Also
Other serialization:
serialize()
empty_face
Description
Alias to the empty integer vector (integer(0L)). Used to indicate the empty face of the tree.
Usage
empty_face
Format
An object of class integer of length 0.
See Also
traverse
enclosing_radius
Description
Computes the enclosing radius of a set of distances.
Usage
enclosing_radius(d)
Arguments
d |
a |
Details
The enclosing radius is useful as an upper bound of the scale parameter for the rips filtration. Scales above the enclosing radius render the Vietoris–Rips complex as a simplicial cone, beyond which the homology is trivial.
k-expansion.
Description
Performs a k-expansion on the 1-skeleton of the complex, adding k-simplices if all combinations of edges are included. Because this operation uses the edges alone to infer the existence of higher order simplices, the expansion assumes the underlying complex is a flag complex.
Usage
expand(st, k = 2)
Arguments
st |
a simplex tree. |
k |
the target dimension of the expansion. |
Generates a face traversal on the simplex tree.
Description
Generates a face traversal on the simplex tree.
Usage
faces(st, sigma)
Arguments
st |
the simplex tree to traverse. |
sigma |
simplex to start the traversal at. |
Find simplices
Description
Returns whether supplied simplices exist in the complex.
Usage
find(st, simplices)
Arguments
st |
a simplex tree. |
simplices |
simplices to insert, either as a vector, a list of vectors, or a column-matrix. See details. |
Details
Traverses the simplex tree looking for simplex, returning whether or not it exists.
simplex can be specified as vector to represent a single simplex, and a list to represent a set of simplices.
Each simplex is sorted before traversing the trie.
If simplices is a vector, it's assumed to be a simplex. If a list, its assumed each element in the list
represents a simplex (as vectors). If the simplices to insert are all of the same dimension, you can also
optionally use a matrix, where each column is assumed to be a simplex.
Value
boolean indicating whether or not simplex exists in the tree.
Usage
st
See Also
insert remove
flag
Description
Creates a filtration of flag complexes
Usage
flag(st, d)
Arguments
st |
a simplex tree. See details. |
d |
a vector of edge weights, or a 'dist' object. |
Details
A flag complex is a simplicial complex whose k-simplices for k >= 2 are completely determined by edges/graph of the complex. This function creates filtered simplicial complex using the supplied edge weights. The resulting complex is a simplex tree object endowed with additional structure; see. Vertices have their weights set to 0, and k-simplices w/ k >= 2 have their weights set to the maximum weight of any of its edges.
Generates vertex ids.
Description
Generates vertex ids representing 0-simplices not in the tree.
Usage
generate_ids(st, n)
Arguments
st |
a simplex tree. |
n |
the number of ids to generate. |
Details
This function generates new vertex ids for use in situations which involve generating new
new 0-simplices, e.g. insertions, contractions, collapses, etc. There are two 'policies' which designate
the generating mechanism of these ids: 'compressed' and 'unique'. 'compressed' generates vertex ids
sequentially, starting at 0. 'unique' tracks an incremental internal counter, which is updated on every
call to generate_ids. The new ids under the 'unique' policy generates the first sequential n
ids that are strictly greater max(counter, max vertex id).
Examples
st <- simplex_tree()
print(st$id_policy)
## "compressed"
st %>% generate_ids(3)
## 0 1 2
st %>% generate_ids(3)
## 0 1 2
st %>% insert(list(1,2,3))
print(st$vertices)
## 1 2 3
st %>% insert(as.list(st %>% generate_ids(2)))
st %>% print_simplices()
# 0, 1, 2, 3, 4
st %>% remove(4)
st %>% generate_ids(1)
# 4
Insert simplices
Description
Inserts simplices into the simplex tree. Individual simplices are specified as vectors, and a set of simplices as a list of vectors.
Usage
insert(st, simplices)
Arguments
st |
a simplex tree. |
simplices |
simplices to insert, either as a vector, a list of vectors, or a column-matrix. See details. |
Details
This function allows insertion of arbitrary order simplices. If the simplex already exists in the tree,
no insertion is made, and the tree is not modified. simplex is sorted before traversing the trie.
Faces of simplex not in the simplex tree are inserted as needed.
If simplices is a vector, it's assumed to be a simplex. If a list, its assumed each element in the list
represents a simplex (as vectors). If the simplices to insert are all of the same dimension, you can also
optionally use a matrix, where each column is assumed to be a simplex.
See Also
find remove
Examples
st <- simplex_tree()
st %>% insert(1:3) ## inserts the 2-simplex { 1, 2, 3 }
st %>% insert(list(4:5, 6)) ## inserts a 1-simplex { 4, 5 } and a 0-simplex { 6 }.
st %>% insert(combn(5,3)) ## inserts all the 2-faces of a 4-simplex
inverse.choose
Description
Inverts the binomial coefficient for general (n,k).
Usage
inverse.choose(x, k)
Arguments
x |
the binomial coefficient. |
k |
the denominator of the binomial coefficient |
Details
Given a quantity x = choose(n, k) with fixed k, finds n.
Value
the numerator of the binomial coefficient, if the Otherwise
Examples
100 == inverse.choose(choose(100,2), k = 2)
# TRUE
12345 == inverse.choose(choose(12345, 5), k = 5)
# TRUE
Is face
Description
Checks whether a simplex is a face of another simplex and is in the complex.
Usage
is_face(st, tau, sigma)
Arguments
st |
a simplex tree. |
tau |
a simplex which may contain |
sigma |
a simplex which may contain |
Details
A simplex \tau is a face of \sigma if \tau \subset \sigma. This function
checks whether that is true. tau and sigma are sorted before comparison.
Value
boolean indicating whether tau is a face of sigma.
See Also
Examples
st <- simplex_tree()
st %>% insert(1:3)
st %>% is_face(2:3, 1:3)
st %>% is_face(1:3, 2:3)
Checks if the simplicial complex is a tree.
Description
This function performs a breadth-first search on the simplicial complex, checking if the complex is acyclic.
Usage
is_tree(st)
Arguments
st |
a simplex tree. |
Examples
st <- simplex_tree()
st %>% insert(list(1:2, 2:3))
st %>% is_tree() # true
st %>% insert(c(1, 3))
st %>% is_tree() # false
Generates a traversal on the k-simplices of the simplex tree.
Description
Generates a traversal on the k-simplices of the simplex tree.
Usage
k_simplices(st, k, sigma = NULL)
Arguments
st |
the simplex tree to traverse. |
k |
the dimension of the skeleton to include. |
sigma |
simplex to start the traversal at. |
Generates a k-skeleton traversal on the simplex tree.
Description
Generates a k-skeleton traversal on the simplex tree.
Usage
k_skeleton(st, k, sigma = NULL)
Arguments
st |
the simplex tree to traverse. |
k |
the dimension of the skeleton to include. |
sigma |
simplex to start the traversal at. |
Generates a level order traversal on the simplex tree.
Description
Generates a level order traversal on the simplex tree.
Usage
level_order(st, sigma = NULL)
Arguments
st |
the simplex tree to traverse. |
sigma |
simplex to start the traversal at. |
Generates a traversal on the link of a given simplex in the simplex tree.
Description
Generates a traversal on the link of a given simplex in the simplex tree.
Usage
link(st, sigma)
Arguments
st |
the simplex tree to traverse. |
sigma |
simplex to start the traversal at. |
Generates a traversal on the maximal of the simplex tree.
Description
Generates a traversal on the maximal of the simplex tree.
Usage
maximal(st, sigma = NULL)
Arguments
st |
the simplex tree to traverse. |
sigma |
simplex to start the traversal at. |
nat_to_sub
Description
Computes the x^th (n choose 2) combination.
Usage
nat_to_sub(x, n, k)
Arguments
x |
non-negative integers in the range |
n |
numerator of the binomial coefficient |
k |
denominator of the binomial coefficient |
Details
The mapping is done via an lexicographically-ordered combinadic mapping.
In general, this function is not intended to be used to generate all (n choose k) combinations in the combinadic mapping.
Value
integer matrix whose columns give the combinadics of x.
References
McCaffrey, J. D. "Generating the mth lexicographical element of a mathematical combination." MSDN Library (2004).
Examples
library(simplextree)
all(nat_to_sub(seq(choose(100,2)), n = 100, k = 2) == combn(100,2))
## Generating pairwise combinadics is particularly fast
## Below: test to generate ~ 45k combinadics (note: better to use microbenchmark)
system.time({
x <- seq(choose(300,2))
nat_to_sub(x, n = 300, k = 2L)
})
## Compare with generating raw combinations
system.time(combn(300,2))
nerve
Description
Compute the nerve of a given cover.
Usage
nerve(st, cover, k = st$dimension, threshold = 1L, neighborhood = NULL)
Arguments
st |
a simplex tree. |
cover |
list of integers indicating set membership. See details. |
k |
max simplex dimension to consider. |
threshold |
the number of elements in common for |
neighborhood |
which combinations of sets to check. See details. |
Details
This computes the nerve of a given cover, adding a k-simplex for each combination of k+1 sets
in the given cover that have at least threshold elements in their common intersection.
If neighborhood is supplied, it can be either 1) a matrix, 2) a list, or 3) a function. Each
type parameterizes which sets in the cover need be checked for to see if they have at least threshold
elements in their common intersection. If a matrix is supplied, the columns should indicate the indices
of the cover to check (e.g if neighborhood = matrix(c(1,2), nrow = 2), then only the first two sets of cover
are tested.). Similarly, if a list is supplied, each element in the list should give the indices to test.
The most flexible option is supplying a function to neighborhood. If a function is passed, it's assumed to
accept an integer vector of k indices (of the cover) and return a boolean indicating whether or not to
test if they have at least threshold elements in their common intersection. This can be used
to filter out subsets of the cover the user knows are The indices are
generated using the same code that performs expand.
plot.Rcpp_Filtration
Description
plot.Rcpp_Filtration
Usage
## S3 method for class 'Rcpp_Filtration'
plot(...)
Arguments
... |
passed to |
Functions
-
plot.Rcpp_Filtration: family of plotting methods.
Plots the simplex tree
Description
Plots the simplex tree
Usage
## S3 method for class 'Rcpp_SimplexTree'
plot(
x,
coords = NULL,
vertex_opt = NULL,
text_opt = NULL,
edge_opt = NULL,
polygon_opt = NULL,
color_pal = NULL,
maximal = TRUE,
by_dim = TRUE,
add = FALSE,
...
)
Arguments
x |
a simplex tree. |
coords |
Optional (n x 2) matrix of coordinates, where n is the number of 0-simplices. |
vertex_opt |
Optional parameters to modify default vertex plotting options. Passed to |
text_opt |
Optional parameters to modify default vertex text plotting options. Passed to |
edge_opt |
Optional parameters to modify default edge plotting options. Passed to |
polygon_opt |
Optional parameters to modify default k-simplex plotting options for k > 1. Passed to |
color_pal |
Optional vector of colors. See details. |
maximal |
Whether to draw only the maximal faces of the complex. Defaults to true. |
by_dim |
Whether to apply (and recycle or truncate) the color palette to the dimensions rather than to the individual simplices. Defaults to true. |
add |
Whether to add to the plot or redraw. Defaults to false. See details. |
... |
unused |
Details
This function allows generic plotting of simplicial complexes using base graphics.
If not (x,y) coordinates are supplied via coords, a default layout is generated via phyllotaxis arrangement. This layout is
not in general does not optimize the embedding towards any usual visualization criteria e.g. it doesn't try to separate connected components,
minimize the number of crossings, etc. For those, the user is recommended to look in existing code graph drawing libraries, e.g. igraphs 'layout.auto' function, etc.
The primary benefit of the default phyllotaxis arrangement is that it is deterministic and fast to generate.
All parameters passed via list to vertex_opt, text_opt, edge_opt, polygon_opt
override default parameters and are passed to points, text, segments,
and polygon, respectively.
If add is true, the plot is not redrawn.
If maximal is true, only the maximal simplices are drawn.
The color_pal argument controls how the simplicial complex is colored. It can be specified in multiple ways.
A vector of colors of length dim+1, where dim=
x$dimensionA vector of colors of length n, where n=
sum(x$n_simplices)A named list of colors
Option (1) assigns every simplex a color based on its dimension.
Option (2) assigns each individual simplex a color. The vector must be specified in level-order
(see ltraverse or examples below).
Option (3) allows specifying individual simplices to draw. It expects a named list, where the names
must correspond to simplices in x as comma-separated strings and whose values are colors. If
option (3) is specified, this method will only draw the simplices given in color_pal.
If length(color_pal) does not match the dimension or the number of simplices in the complex,
the color palette is recyled and simplices are as such.
Examples
## Simple 3-simplex
st <- simplex_tree() %>% insert(list(1:4))
## Default is categorical colors w/ diminishing opacity
plot(st)
## If supplied colors have alpha defined, use that
vpal <- rainbow(st$dimension + 1)
plot(st, color_pal = vpal)
## If alpha not supplied, decreasing opacity applied
plot(st, color_pal = substring(vpal, first=1, last=7))
## Bigger example; observe only maximal faces (+vertices and edges) are drawn
st <- simplex_tree(list(1:3, 2:5, 5:9, 7:8, 10))
plot(st, color_pal = rainbow(st$dimension + 1))
## If maximal == FALSE, every simplex is drawn (even on top of each other)
vpal <- rainbow(st$dimension + 1)[c(1,2,5,4,3)]
pal_alpha <- c(1, 1, 0.2, 0.35, 0.35)
vpal <- sapply(seq_along(vpal), function(i) adjustcolor(vpal[i], alpha.f = pal_alpha[i]))
plot(st, color_pal = vpal, maximal = FALSE)
## You can also color each simplex individually by supplying a vector
## of the same length as the number of simplices.
plot(st, color_pal = sample(rainbow(sum(st$n_simplices))))
## The order is assumed to follow the level order traversal (first 0-simplices, 1-, etc.)
## This example colors simplices on a rainbow gradient based on the sum of their labels
si_sum <- straverse(st %>% level_order, sum)
rbw_pal <- rev(rainbow(50, start=0,end=4/6))
plot(st, color_pal=rbw_pal[cut(si_sum, breaks=50, labels = FALSE)])
## This also makes highlighting simplicial operations fairly trivial
four_cofaces <- as.list(cofaces(st, 4))
coface_pal <- straverse(level_order(st), function(simplex){
ifelse(list(simplex) %in% four_cofaces, "orange", "blue")
})
plot(st, color_pal=unlist(coface_pal))
## You can also give a named list to draw individual simplices.
## **Only the maximal simplices in the list are drawn**
blue_vertices <- structure(as.list(rep("blue", 5)), names=as.character(seq(5, 9)))
plot(st, color_pal=append(blue_vertices, list("5,6,7,8,9"="red")))
Generates a preorder traversal on the simplex tree.
Description
Generates a preorder traversal on the simplex tree.
Usage
preorder(st, sigma = NULL)
Arguments
st |
the simplex tree to traverse. |
sigma |
simplex to start the traversal at. |
print.st_traversal
Description
print.st_traversal
Usage
## S3 method for class 'st_traversal'
print(x, ...)
Arguments
x |
traversal object. |
... |
unused. |
Print simplices to the console
Description
Prints simplices in a formatted way
Prints a traversal, a simplex tree, or a list of simplices to the R console, with
options to customize how the simplices are printed. The format must be one of
"summary", "tree", "cousins", "short", "column", or "row", with the default being "short".
In general, the "tree" and "cousins" format give more details on the structure of the trie,
whereas the other formats just change how the given set of simplices are formatted.
The "tree" method prints the nodes grouped by the same last label and indexed by depth.
The printed format is:
[vertex] (h = [subtree height]): [subtree depth]([subtree])
Where each lists the top node (vertex) and its corresponding subtree. The
subtree height displays the highest order k-simplex in that subtree. Each
level in the subtree tree is a set of sibling k-simplices whose order is given
by the number of dots ('.') proceeding the print level.
The "cousin" format prints the simplex relations used by various algorithms to speed
up finding adjacencies in the complex. The cousins are grouped by label and depth.
The format looks like:
(last=[label], depth=[depth of label]): [simplex]
This function is useful for understanding how the simplex tree is stored, and for debugging purposes.
Usage
print_simplices(
st,
format = c("summary", "tree", "cousins", "short", "column", "row")
)
Arguments
st |
a simplex tree. |
format |
the choice of how to format the printing. See details. |
reindexes vertex ids
Description
This function allows one to 'reorder' or 'reindex' vertex ids.
Usage
reindex(st, ids)
Arguments
st |
a simplex tree. |
ids |
vector of new vertex ids. See details. |
Details
The ids parameter must be a sorted integer vector of new ids with length matching the
number of vertices. The simplex tree is modified to replace the vertex label at index i with
ids[i]. See examples.
Examples
st <- simplex_tree()
st %>% insert(1:3) %>% print_simplices("tree")
# 1 (h = 2): .( 2 3 )..( 3 )
# 2 (h = 1): .( 3 )
# 3 (h = 0):
st %>% reindex(4:6) %>% print_simplices("tree")
# 4 (h = 2): .( 5 6 )..( 6 )
# 5 (h = 1): .( 6 )
# 6 (h = 0):
Remove simplices
Description
Removes simplices from the simplex tree. Individual simplices are specified as vectors, and a set of simplices as a list of vectors.
Usage
remove(st, simplices)
Arguments
st |
a simplex tree. |
simplices |
simplices to insert, either as a vector, a list of vectors, or a column-matrix. See details. |
Details
This function allows removal of a arbitrary order simplices. If simplex already exists in the tree,
it is removed, otherwise the tree is not modified. simplex is sorted before traversing the trie.
Cofaces of simplex are also removed.
If simplices is a vector, it's assumed to be a simplex. If a list, its assumed each element in the list
represents a simplex (as vectors). If the simplices to insert are all of the same dimension, you can also
optionally use a matrix, where each column is assumed to be a simplex.
See Also
find remove
rips
Description
Constructs the Vietoris-Rips complex.
Usage
rips(d, eps = enclosing_radius(d), dim = 1L, filtered = FALSE)
Arguments
d |
a numeric 'dist' vector. |
eps |
diameter parameter. |
dim |
maximum dimension to construct up to. Defaults to 1 (edges only). |
filtered |
whether to construct the filtration. Defaults to false. See details. |
Serializes the simplex tree.
Description
Provides a compressed serialization interface for the simplex tree.
Usage
serialize(st)
Arguments
st |
a simplex tree. |
Details
The serialize/deserialize commands can be used to compress/uncompress the complex into
smaller form amenable for e.g. storing on disk (see saveRDS) or saving for later use.
The serialization.
See Also
Other serialization:
deserialize()
Examples
st <- simplex_tree(list(1:5, 7:9))
st2 <- deserialize(serialize(st))
all.equal(as.list(preorder(st)), as.list(preorder(st2)))
# TRUE
set.seed(1234)
R <- rips(dist(replicate(2, rnorm(100))), eps = pnorm(0.10), dim = 2)
print(R$n_simplices)
# 100 384 851
## Approx. size of the full complex
print(utils::object.size(as.list(preorder(R))), units = "Kb")
# 106.4 Kb
## Approx. size of serialized version
print(utils::object.size(serialize(R)), units = "Kb")
# 5.4 Kb
## You can save these to disk via e.g. saveRDS(serialize(R), ...)
Simplex Tree
Description
Simplex tree class exposed as an Rcpp Module.
Usage
simplex_tree(simplices = NULL)
Arguments
simplices |
optional simplices to initialize the simplex tree with. See |
Details
A simplex tree is an ordered trie-like structure specialized for storing and doing general computation
simplicial complexes. Here is figure of a simplex tree, taken from the original paper (see 1):
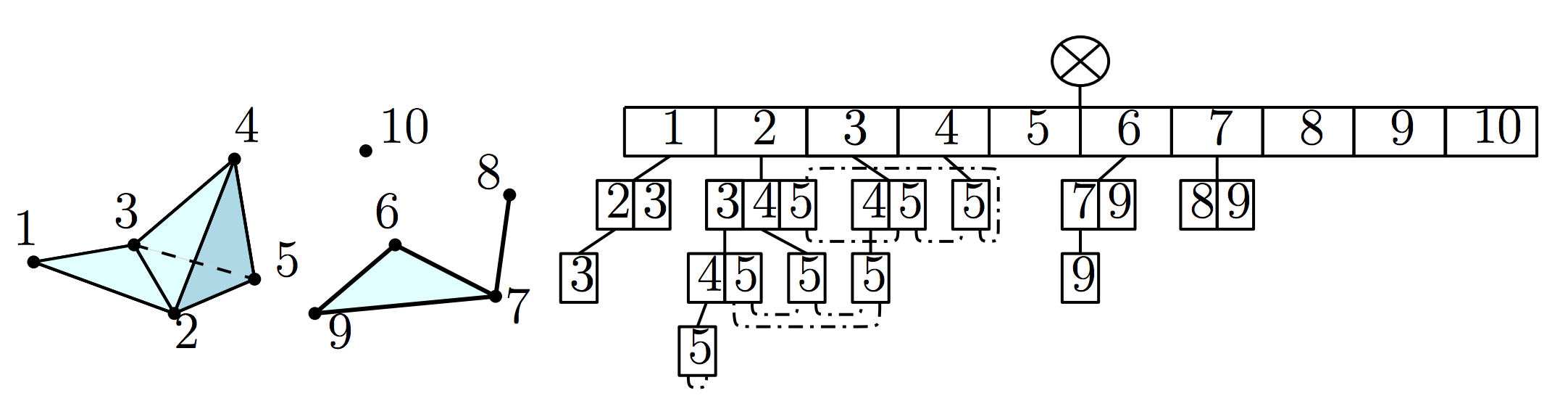
The current implementation provides a subset of the functionality described in the paper.
Value
A queryable simplex tree, as a Rcpp_SimplexTree object (Rcpp module).
Fields
n_simplicesA vector, where each index k denotes the number (k-1)-simplices.
dimensionThe dimension of the simplicial complex.
Properties
Properties are actively bound shortcuts to various methods of the simplex tree that may be thought of as fields. Unlike fields, however, properties are not explicitly stored: they are generated on access.
- $
id_policy The policy used to generate new vertex ids. May be assigned "compressed" or "unique". See
generate_ids.- $
vertices The 0-simplices of the simplicial complex, as a matrix.
- $
edges The 1-simplices of the simplicial complex, as a matrix.
- $
triangles The 2-simplices of the simplicial complex, as a matrix.
- $
quads The 3-simplices of the simplicial complex, as a matrix.
- $
connected_components The connected components of the simplicial complex.
Methods
- $
as_XPtr Creates an external pointer.
- $
clear Clears the simplex tree.
- $
generate_ids Generates new vertex ids according to the set policy.
- $
degree Returns the degree of each given vertex.
- $
adjacent Returns vertices adjacent to a given vertex.
- $
insert Inserts a simplex into the trie.
- $
remove Removes a simplex from the trie.
- $
find Returns whether a simplex exists in the trie.
- $
collapse Performs an elementary collapse.
- $
contract Performs an edge contraction.
- $
expand Performs an k-expansion.
- $
traverse Traverses a subset of the simplex tree, applying a function to each simplex.
- $
ltraverse Traverses a subset of the simplex tree, applying a function to each simplex and returning the result as a list.
- $
is_face Checks for faces.
- $
is_tree Checks if the simplicial complex is a tree.
- $
as_list Converts the simplicial complex to a list.
- $
as_adjacency_matrix Converts the 1-skeleton to an adjacency matrix.
- $
as_adjacency_list Converts the 1-skeleton to an adjacency list.
- $
as_edgelist Converts the 1-skeleton to an edgelist.
Author(s)
Matt Piekenbrock
References
Boissonnat, Jean-Daniel, and Clement Maria. "The simplex tree: An efficient data structure for general simplicial complexes." Algorithmica 70.3 (2014): 406-427.
Examples
## Recreating simplex tree from figure.
st <- simplex_tree()
st %>% insert(list(1:3, 2:5, c(6, 7, 9), 7:8, 10))
plot(st)
## Example insertion
st <- simplex_tree(list(1:3, 4:5, 6)) ## Inserts one 2-simplex, one 1-simplex, and one 0-simplex
print(st)
# Simplex Tree with (6, 4, 1) (0, 1, 2)-simplices
## More detailed look at structure
print_simplices(st, "tree")
# 1 (h = 2): .( 2 3 )..( 3 )
# 2 (h = 1): .( 3 )
# 3 (h = 0):
# 4 (h = 1): .( 5 )
# 5 (h = 0):
# 6 (h = 0):
## Print the set of simplices making up the star of the simplex '2'
print_simplices(st %>% cofaces(2))
# 2, 2 3, 1 2, 1 2 3
## Retrieves list of all simplices in DFS order, starting with the empty face
dfs_list <- ltraverse(st %>% preorder(empty_face), identity)
## Get connected components
print(st$connected_components)
# [1] 1 1 1 4 4 5
## Use clone() to make copies of the complex (don't use the assignment `<-`)
new_st <- st %>% clone()
## Other more internal methods available via `$`
list_of_simplices <- st$as_list()
adj_matrix <- st$as_adjacency_matrix()
# ... see also as_adjacency_list(), as_edge_list(), etc
sub_to_nat
Description
Given a combination x, computes its position out of all lexicographically-ordered (n choose 2) combinations.
Usage
sub_to_nat(x, n)
Arguments
x |
matrix whose columns represent |
n |
numerator of the binomial coefficient |
Details
The mapping is done via an lexicographically-ordered combinadic mapping.
Value
integer vector of the positions of the given combinations.
References
McCaffrey, J. D. "Generating the mth lexicographical element of a mathematical combination." MSDN Library (2004).
threshold
Description
Thresholds a given filtered simplicial complex.
Usage
threshold(st, index = NULL, value = NULL)
Arguments
st |
simplex tree. |
index |
integer index to threshold to. |
value |
numeric index to threshold filtration. |
traverse
Description
Traverses specific subsets of a simplicial complex.
Usage
traverse(traversal, f, ...)
straverse(traversal, f, ...)
ltraverse(traversal, f, ...)
Arguments
traversal |
the type of traversal. |
f |
the function to apply to each simplex. |
... |
unused. |
Details
traverse allows for traversing ordered subsets of the simplex tree.
The specific subset and order are determined by the choice of traversal: examples include
the preorder traversal, the cofaces traversal, etc. See the links below.
Each simplex in the traversal is passed as the first and only argument to f, one per simplex in the traversal.
traverse does nothing with the result; if you want to collect the results of applying f to each simplex
into a list, use ltraverse (or straverse), which are meant to be used like lapply
and sapply, respectively.
Value
NULL; for list or vector-valued returns, use ltraverse and straverse respectively.
Examples
## Starter example complex
st <- simplex_tree()
st %>% insert(list(1:3, 2:5))
## Print out complex using depth-first traversal.
st %>% preorder() %>% traverse(print)
## Collect the last labels of each simplex in the tree.
last_labels <- st %>% preorder() %>% straverse(function(simplex){ tail(simplex, 1) })
UnionFind
Description
Union find structure exposed as an Rcpp Module.
Usage
union_find(n = 0L)
Arguments
n |
Number of elements in the set. |
Value
A disjoint set, as a Rcpp_UnionFind object (Rcpp module).
Methods
- $
print.simplextree S3 method to print a basic summary of the simplex tree.
Author(s)
Matt Piekenbrock